前言

今天要來介紹隨機變數(Random Variable)，統計的母體是某個要預測事物的所有可能發生結果的集合，隨機變數則是一個不確定性事件結果的數值函數(Function)，也就是說把不確定性事件的結果用數值來表示，即為隨機變數。根據隨機變數可能取值的結果，可以分成兩種：

1. 離散型隨機變數(Discrete Random Variable)：隨機變數取值的範圍有限個(ex 擲硬幣只有兩種結果，所以取擲的範圍有限制)
2. 連續型隨機變數(Continuous Random Variable)：隨機變數可以在一個區間上任意取值(ex 股票中的收益率就是連續型隨機變數)

離散型隨機變數(Discrete Random Variable)：

設X是一個隨機變數，如果它全部可能的取值只有有限個或可數無窮個，則稱X為一個離散型隨機變數。
假設現在有n個數據，每個數據發生的機率即為
概率質量函數(Probability Mass Function)： P(X = xi) = Pi,i = 1,2,...
使用Python中的choice()來產生特定機率隨機數

choice(a, size=None, p=None)

a：隨機變數所有可能的取值
size：產生的陣列大小
p：與a同等大小，指定每種數據發生的機率

import numpy as np
import pandas as pd

ironman = np.random.choice([1,2,3,4,5], size=1000, p=[0.25,0.1,0.35,0.2,0.1])
valueCount = pd.Series(ironman).value_counts()
print('valueCount/1000---->', valueCount/1000)

# 輸出結果
valueCount/1000----> 3    0.365
1    0.245
4    0.191
5    0.119
2    0.080

從上面的例子可以看到，原本設定，[1,2,3,4,5]出現的機率為[0.25,0.1,0.35,0.2,0.1]，使用choice隨機產生1000個數字其中[1,2,3,4,5]所佔的機率為[0.245,0.080,0.365,0.191,0.119]兩邊所呈現的機率很相近。當樣本越高，結果會越接近設定的機率。

連續型隨機變數(Continuous Random Variable)：

即在一定區間內變數取值有無限個，或數值無法一一列舉出來。用來表示某個區間內每個數值所發生的機率為
機率密度函數(Probability Density Function)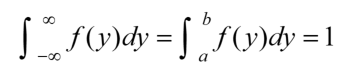

以下圖為例，在5~6發生的機率即為紅色的面積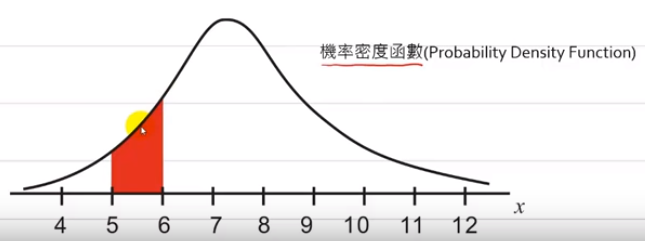

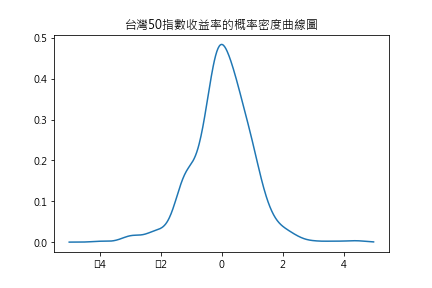
下面使用台灣50的日收益率來顯示機率分佈的過程

from scipy import stats
import matplotlib.pyplot as plt
%matplotlib inline

tw50 = pd.read_csv('tw50.csv', sep='\t', index_col='Date')

tw50_gaussian = stats.kde.gaussian_kde(tw50.ROI)
# gaussian_kde-> 高斯核函數，kde 是核函數密度估計
x_value = np.arange(-5,5,0.02)

fig = plt.figure()
plt.subplot()
plt.plot(x_value, tw50_gaussian(x_value))
plt.title("台灣50指數收益率的概率密度曲線圖")

期望值和變異數

期望值(Expectation)是隨機變數所有可能取值結果的均值，用來呈現母體的中心位置：
間斷型公式：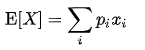
連續型公式：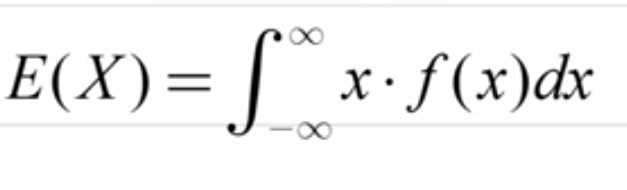
將所有出現X樣本值*樣本機率相加
變異數：
間斷型公式：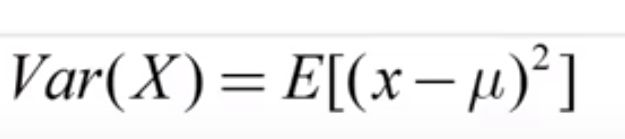
連續型公式：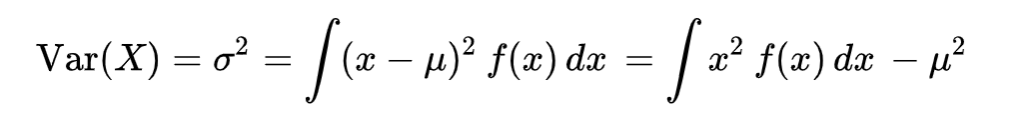

二項分佈

二項實驗：做了n次的試驗只有兩種結果(成功、失敗)，p(成功的機率)+q(失敗的機率) = 1，每次試驗都是相互獨立的。X表示成功的次數其公式如下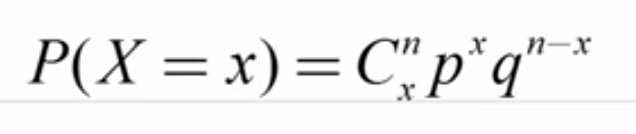

Numpy中產生二項分佈隨機數的函式如下：

binomial(n,p,size)

n：二項實驗的次數
p: 表示成功的機率
size: 隨機產生的數量

投擲100次硬幣，正面朝上的對應的機率為0.5，對應的分佈為b(100,0.5)，之後產生20個來源於該二項分佈的隨機數

np.random.binomial(100,0.5,20)

# 輸出結果
array([56, 49, 49, 52, 44, 50, 40, 52, 46, 49, 54, 46, 55, 49, 57, 45, 45,
       54, 53, 47])

從上述的例子引申為，假設每次擲骰子正面朝上的機率為0.5，擲100次，有20次正面朝上的機率為

from scipy import stats
stats.binom.pmf(20,100,0.5)

# 輸出結果
4.228163267601253e-10

二項式分佈在金融市場中的應用

ret = tw50.ROI  #台灣50的收益率數據
ret.index = pd.to_datetime(tw50.index)
ret1 = ret['2016']

#台灣50上漲的機率p
p = len(ret1[ret>0]) /len(ret1)
print('p----->', p)

#預估未來20個交易日中，有7個是上漲的機率
prob =stats.binom.pmf(6,20,p)
print('prob----->', prob)

# 輸出結果
p-----> 0.5327868852459017
prob-----> 0.02093703958512302

常態分佈

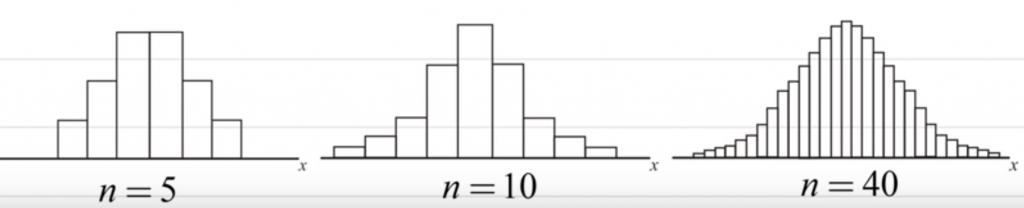
二項式分配指的是，試驗次數n越大的時候，則無論成功機率p值為何，其分配會越來越呈現對稱的情形，當二項分佈的np > 5 且 nq > 5 時，通常會以常態分佈來估計機率。二項分配是一種間斷型的分配，從下圖可以得知當n越來越大時會越來越像常態分佈

之前的章節

• 安裝環境
  • 安裝Anaconda
  • 安裝Jupyter notebook
• Seaborn
  • distplot、heatmap()
  • 樣式設定
• 統計
  • 統計基礎
• 程式碼位置
  • github
    因為作者本身也是第一次學習Python和寫程式文章，所以編排上會有點亂，觀念可能也會錯誤，如果有疑問可以提出一起討論。