前言

在監督式學習中，我們可以將收集而來的資料切割為訓練集與測試集來尋找表現最好的模型，而這兩種資料集就像字面上的意思一樣，訓練集是用來訓練模型，測試集是用來測試訓練好的模型效果。然而，一般情況常見的處理方式為隨機抽樣(Random Sampling)將資料依特定比例切割為訓練集與測試集，但若利用分層抽樣(Stratified Sampling)的方式盡量使某類別在測試集與訓練集的比例相近，得到具有代表性的測試集後或許可以找出表現較好的模型，若是處理分類的問題時更需要注意這樣的問題。

匯入套件與資料

這是一筆來自加州1990年人口普查的資料，在這筆資料中包含10個變數與20640個樣本，其中感興趣的變數為房價的中位數(median_house_value)。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import StratifiedShuffleSplit

housing = pd.read_csv("https://raw.githubusercontent.com/ageron/handson-ml2/master/datasets/housing/housing.csv")

housing.head()

• 利用train_test_split()隨機抽樣生成訓練集與測試集

train_set, test_set = train_test_split(housing, test_size=0.2, random_state=42)
#test_size設定測試集的比例、random_state設定種子使每次抽樣結果一樣

test_set.head()

分層抽樣(Stratified Sampling)

假設我們已知收入的中位數(median_income)是影響感興趣變數(median_house_value)的一個重要因素，我們需要確保切割出來的測試集有足夠的代表性可以代表原來的資料，不過因median_income為一個連續型的變數，因此我們可以幾個切點建立幾個屬於median_income的類別，觀察其類別的資料比例。

• 觀察median_income資料分佈情況

housing["median_income"].hist(bins = 50)
plt.title("median_income")
plt.show()

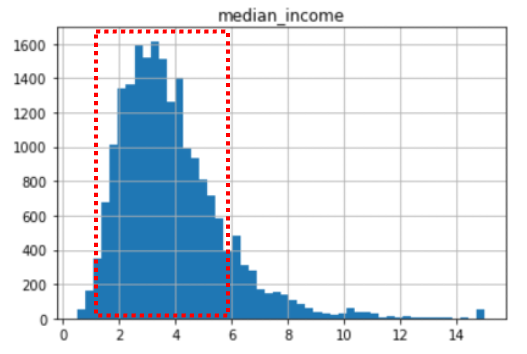
• 利用pd.cut()由median_income的分組建立一個新的變數income_cat，分組時也要注意每組的數量不能太少，由上圖可以觀察到大部分的房租價錢落在1.5 ~ 6.0，因此我們可以將median_income切割成五個類別，分別為0~1.5、1.5~3.0、3.0~4.5、4.5~6.0、6.0~inf。

housing["income_cat"] = pd.cut(housing["median_income"],
                               bins=[0., 1.5, 3.0, 4.5, 6., np.inf],
                               labels=[1, 2, 3, 4, 5])

• 觀察分組後每組的個數

housing["income_cat"].value_counts()

housing["income_cat"].hist()
plt.title("income_cat")
plt.show()

• 利用分組後各組的樣本數比例生成訓練集與測試集

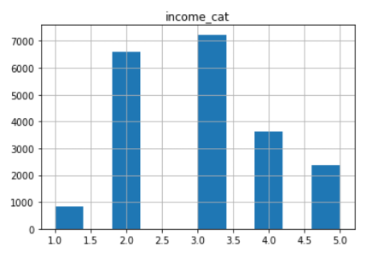
split = StratifiedShuffleSplit(n_splits = 1, test_size = 0.2, random_state = 42) 
#每個分組都取20%放入測試集

for train_index, test_index in split.split(housing, housing["income_cat"]):
    strat_train_set = housing.loc[train_index]
    strat_test_set = housing.loc[test_index]

比較兩種抽樣方式

def income_cat_proportions(data):
    return data["income_cat"].value_counts() / len(data)

train_set, test_set = train_test_split(housing, test_size = 0.2, random_state=42)

compare_props = pd.DataFrame({
                "Overall": income_cat_proportions(housing),
                "Stratified": income_cat_proportions(strat_test_set),
                "Random": income_cat_proportions(test_set)
                }).sort_index()

compare_props

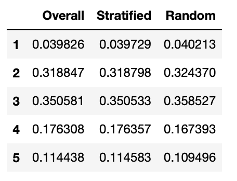
可以發現利用分層抽樣生成的測試集其收入類別(income_cat)的比例與原來的資料較相近，同時分層抽樣的結果也會使訓練集與測試集收入類別的比例比較相似，因此訓練出來的模型層能有更準確的結果，在處理分類問題時更要注意這樣的情況，如果訓練集與測試集要分類的類別標籤比例不一致時，可能會使模型的準確度降低。

資料參考

https://www.kaggle.com/datasets/camnugent/california-housing-prices