前言與介紹

K-近鄰演算法(K-Nearest Neighbors)，簡稱KNN，屬於機器學習中監督式學習(supervised learning)的無母數方法，可以用於處理分類與迴歸的問題。概念為機器學習中較為簡單且直觀的演算法，原理是在給定一個input(x)並找尋與k個最接近的訓練集資料後，投票預測其類別或數值。換句話說就是物以類聚的概念，一群好朋友中若10個人有8個是有錢人，那麼你也十之八九是個有錢人。其中，分類的問題由x的k個最接近的鄰居「投票」決定其x的類別，例如k=1時，x的預測值就會由最相似的訓練資料點所決定。迴歸問題為找到k個最接近鄰居之間的平均值，例如k=3時，x的預測值就是3個鄰居數值的平均。因此，KNN的基本假設為：有相似features的資料，output的結果也會相似。

分類問題

假設資料(y為類別資料，共三組)，k = 2：
x = {1, 2, 3, 4, 5, 6, 7}
y = {1, 2, 2, 3, 3, 1, 2}
此時input(xi)為2.5，最接近的兩個鄰居為x = 2, 3，類別都為第2組，因此xi的預測組別為第2組

迴歸問題

假設資料(y為連續資料)，k = 2：
x = {1, 2, 3, 4, 5, 6, 7}
y = {1, 4, 10, 3, 3, 1, 2}
此時input(xi)為2.5，最接近的兩個鄰居為x = 2, 3，數值分別為4與10，因此xi的預測值為(4 + 10) / 2 =7

數學公式(迴歸)

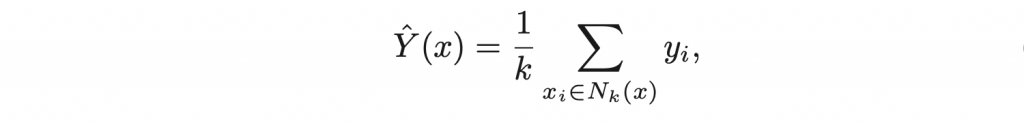
為訓練集資料中與input x最接近的k個鄰居，最後將k個鄰居的反應變數y取平均值。

KNN的執行步驟

1. 計算每個點之間的距離(因此KNN的計算量很大)
2. 選擇一個適當的k值決定鄰居個數
3. 投票決定預測類別或平均數值

計算距離

最常使用來衡量資料之間距離(metric)的方法為歐式距離(Euclidean distance):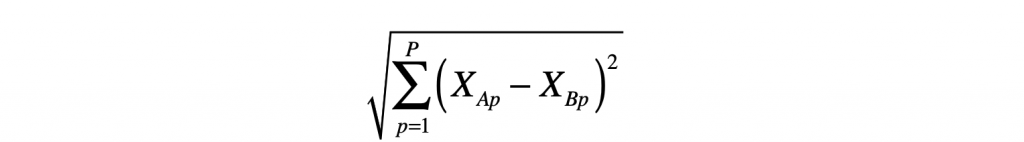

還有其他計算距離的方法，例如曼哈頓距離(Manhattan Distance)與馬哈拉諾比斯距離(Mahalanobis Distance)等，使用者可以根據想選用的衡量方式來計算距離。然而，解釋變數(x)若為類別變數時也需要使用其他衡量距離的方法，例如漢明距離(Hamming distance)等。

KNN需要注意的問題

• k的選擇：
  在KNN的模型中，隨著K越大模型會變得越簡單，K越小則模型越複雜。當不小心使用了太過於複雜的模型時，將會導致overfitting的問題產生，例如K=1的模型在訓練集資料中一定會是表現得最好的，但是在測試集資料的表現就會顯得很差，因此執行KNN的演算法中常常需要利用交叉驗證(cross-validation)的方法來決定適當的K。另外，K的選擇常常會是奇數來避免投票時平手的情形。
• 高維度的資料：
  當資料的維度很高時，或稱為解釋變數(x)很多時，樣本數不夠多的時候可能會造成問題，稱為Curse of dimensionality。例如在1維時，30筆資料可能可以把模型訓練的很好，到了2維就需要30x30筆資料才能訓練好，以此類推，到了維度很高但樣本數很少時，資料在空間中就會顯得非常稀疏(sparse)，在這樣的狀況下利用KNN選擇鄰居來建立模型時就會顯得困難，因為稀疏的環境下，每個資料點都變個更遠，對於相似特徵的資料點很接近的假設被打破，且在高維度空間下計算距離需要花費更多的成本，此時可以利用降維的方式改善。