前言與介紹

在分類問題中除了邏輯斯迴歸模型外，還有另一種常用的方法為線性判別分析(Linear discriminant analysis, LDA)，主要概念是利用貝氏定理(Bayes theorem)的想法來進行分類。假設總共有K個類別，例如以下的式子：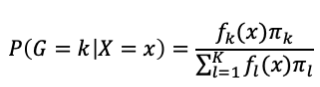

• 為後驗機率(posterior probability)
• 為解釋變數X在第k類中的機率密度函數(pdf)
• 為第k類的先驗機率(prior probability)
• 
  利用此定義下的貝氏定理來分類的方法還有Quadractic discriminant analysis (QDA)與Naive Bayes model等，這些方法在於對機率密度函數(pdf)的假設不同。

線性判別分析(Linear Discriminant Analysis)

在LDA中假設機率密度函數(pdf)服從多維度常態分佈(multivariate normal distribution, MVN)，也就是假設每個類別中的解釋變數服從MVN，且要求每類之間的共變異數(covariace)一樣：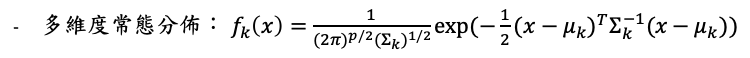


由這兩個假設後，可以比較特定兩個類別k, l的情況：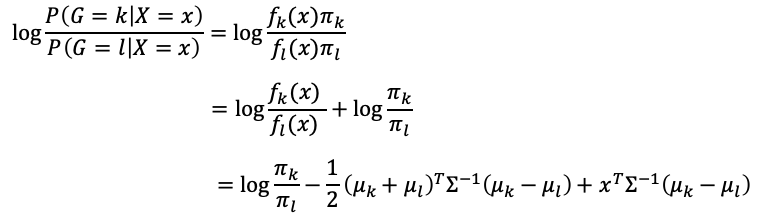

可以由大於0或小於0來判斷哪一個類別可能性較大，其判斷式為x的線性函數

結語

LDA的判斷式與邏輯斯迴歸模型的形式非常相似，不過LDA針對每一類資料多了多維度常態分佈的假設。當每個類別資料經檢查或檢定後與常態相似且樣本數較小時，LDA表現會比邏輯斯迴歸更好，但一般來說邏輯斯迴歸模型因為假設較少，因此可能會更符合一般的情況。當決策邊界(用以分割資料來分類的邊線)為線性時，LDA與邏輯斯迴歸模型表現會不錯。決策邊界非線性時，QDA與Naive Bayes表現較好。然而，若決策邊界較複雜時，無母數(nonparametric)的KNN會有較佳的表現。