前言與介紹

決策樹(Decision tree)在機器學習中是一種容易理解但強大的演算法，可以用來處理分類以及迴歸的問題(Classification and Regression Tree, CART)，強大的地方在於決策樹對於資料沒有什麼假設，可以處理許多複雜的資料集，屬於一種無母數方法。決策樹簡單來說就是利用一連串的if-else的方法，也就是將input或解釋變數X進行分割的方式來做最後結果的預測。後面幾天的內容會提到利用集成學習(Enemble learning)的方法生成很多棵樹將decision tree的預測準確率提高，例如boosting、bagging與random forest。

基本名詞定義

迴歸樹(Regression Tree)

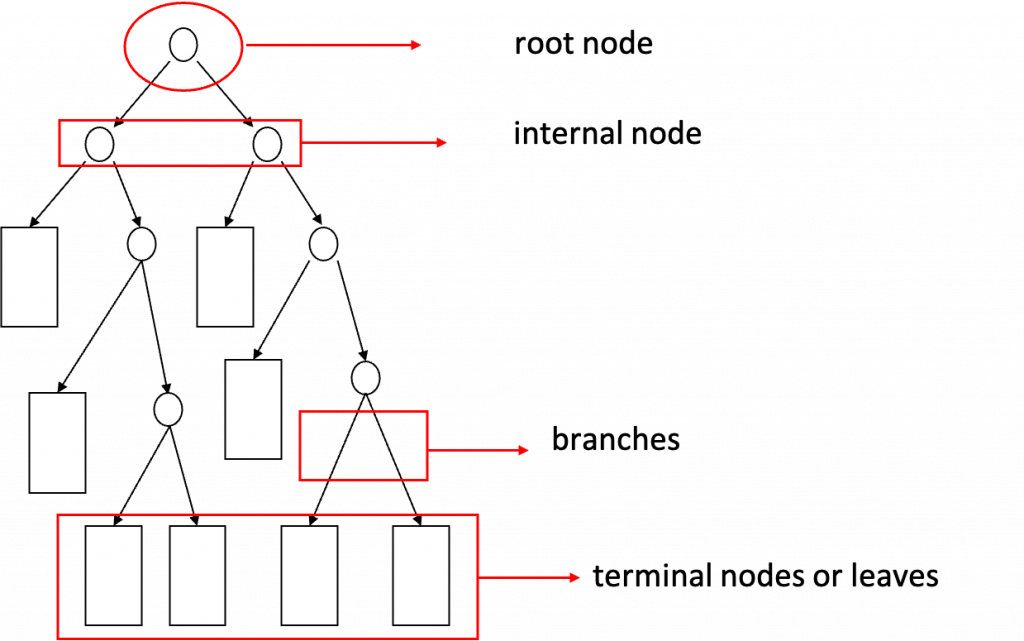
• 簡單的例子說明：
  用來處理迴歸問題(反應變數或outcome為連續資料)的決策樹。例如一筆棒球大聯盟的資料，我們想利用其中的年資(Years)與前一年的打擊命中次數(Hits)預測球員的薪資(Salary)，薪資事先移除了遺失值且利用log轉換(使資料更接近鐘型分佈)當成最後想預測的變數。如下圖，第一個分割方式是年資是否小於4.5年，符合的話就繼續走右邊，否就會走左邊，到了最後的terminal nodes等於把薪資的資料分成了三個組別R1、R2與R3(將年資與打擊次數這兩個變數形成的空間切割為三組)，而這三個組別各自以薪資的平均數值當作預測值(如圖中的5.11、6.00、6.74)。

  

  

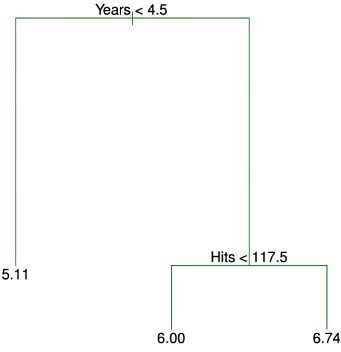
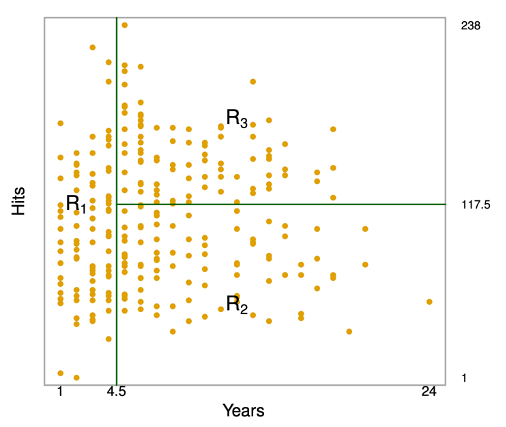
• 決策樹解釋：
  由決策樹的結果可以判斷年資為影響薪資最重要的變數，年資較短球員的薪資低於年資較長的球員，且年資較短的球員在前一年的命中次數對他的薪資影響不大。 但在已經在大聯盟效力五年或以上的球員中，前一年的打擊命中數確實會影響薪水，打擊命中次數多的球員往往薪水更高。 此決策樹的好處是比起一般的迴歸模型更容易解釋、假設更少，並且具有能夠視覺化的優勢。

• 建立決策樹步驟：

1. 將解釋變數形成的空間分割為J個區塊。
2. 針對每個區塊內的資料以平均值來當作估計值

• 如何根據上述兩點執行？目標是每個區塊中的估計值(區塊中資料的平均值)與真實數值差距越小越好：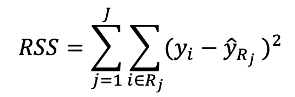
  
  但是要將每種可能的分割情形都計算一次上述的式子，以目前的電腦運算效率看來是不可行的，因此需要一種由上而下在每個步驟中都選擇當時最好的設定(greedy)的方式，依次分割空間來建立決策樹。首先，選擇一個解釋變數與一個切點s將此解釋變數切割為兩個區塊R1與R2。

  

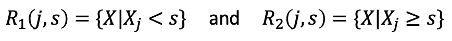
  這裡的目的是要找到一組j與s可以滿足下式分割後的RSS，也就是重複針對每個變數執行這個步驟，在每個變數中找到使得下式最小的切點s，再比較這些變數中哪個能夠有最小的數值：

  

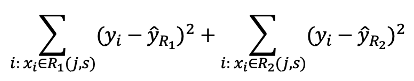
  決定好第一個下手的變數且分割為兩個區塊之後，繼續尋找下一個變數分割其中一個區塊，一直重複到符合停止標準(例如直到每個區塊包含的資料不超過五筆)，建構完這些區塊後就可以將每個區塊中的平均值來作為預測值。

參考資料與圖片來源：
An Introduction to Statistical Learning