前言

昨天的內容提到針對迴歸的問題如何建立決策樹模型，可以針對訓練集的資料有一個好的預測，但是以昨天提到的方式建立一個完美的決策樹模型後，會使得整棵樹的分支很多也就是整個模型變得非常複雜，而導致overfitting的問題。因此就需要針對決策樹修剪(pruning)的方法來降低模型的複雜度。今天也會包含決策樹處理分類問題的方式。

修剪(Pruning)

較小顆的樹或分割空間()較少的決策樹可以有比較好的解釋力或較低的variance，缺點是有比較大的bias。這樣的模型可以在生成決策樹時加上一個選擇變數分割時RSS要下降達到某個閾值才會進行分割(分枝)使生成的決策樹規模較小，但這樣的方式可能會造成一些好的分割方式被忽略了。

• Cost complexity pruning (weakest link pruning)
  因此比較好的策略是讓決策樹生長到極致之後，再利用修剪的方式來降低模型的複雜度獲得子樹(subtree)。進行修剪的目的是想在測試資料集中獲得較低的錯誤(test error)，這時候可以使用k-fold CV來估計subtree在測試集的錯誤，不過要將每個可能的subtree都跑一次驗證會花費太多資源，因此需要一種方法來選擇一部份的subtree來測試增加運算效率。Cost complexity pruning利用下式當成一個新的RSS，也就是要最小化的目標函數，找到tuning parameter 使下式越小越好，而每一種的數值就會對應到一種subtree，當時為完整沒有被修剪過的決策樹，利用交叉驗證的方法可以找到在測試集表現最好的，此方法就像迴歸模型中的lasso可以幫助降低模型的複雜度。
  
• 為terminal node的個數
• 為第m個terminal node對應的區塊
• 為tuning parameter

分類樹(Classification Tree)

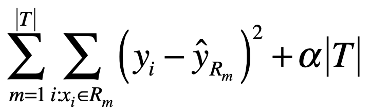
決策樹在處理分類問題的概念與迴歸樹相似，在迴歸樹中以分割後每個區塊中的平均值來決定最後的預測值，而分類樹以出現最多次的類別當成最後的預測。並在分類樹中已經不適合利用迴歸樹中最小化RSS的方式決定模型，以分類的錯誤率(classification error rate)來當成模型選擇的標準較為適合，根據每個區塊中類別比例最高的來決定最後的分類，下式為分類錯誤率。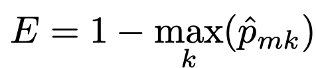

• 為第m個區塊中第k個類別的比例

除了分類錯誤率外還有兩種常見的指標：

1. Gini index: 為K個類別的變異數總和，可以發現在越接近1或0時，Gini index的數值會越小。因為這個性質Gini index也可以當作資料中的純度(purity)，數值越小表示資料大多來自同個類別。
   
2. Cross-entropy(熵): 與Gini index非常相似，當越接近1或0時，cross-entropy將接近0。
   

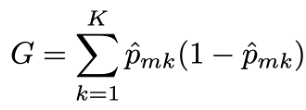
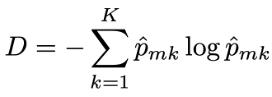
在構建分類樹時，通常使用以上兩種指標來評估特定分割好壞，因為這兩種方法對節點純度的變化比分類錯誤率更敏感。且以上兩種指標是可微的(differentiable)，因此也更適合利用於最佳化的問題。 修剪決策樹時可以使用這三種方法中的任何一種，但如果目標是最終修剪決策樹的預測準確度，則分類錯誤率更適合。

小結

先前提到的監督式學習方法中，不論是迴歸問題或分類問題常用的幾個模型，決策樹相較之下擁有更容易解釋的模型架構也更容易理解，甚至有許多人認為這樣的架構更能反映人類的決策過程。缺點是決策樹的準確率還是不及其他監督式學習的方法，但若有了集成學習(enemble learning)的方式生成更多決策樹，或許可以顯著提升模型的準確度，接下來幾天也會提到相關的內容。

參考資料：
An Introduction to Statistical Learning