前言

線性迴歸(Linear Regression)是監督式學習中相對比較簡單且容易理解的方法，一種用來建立X(解釋變數/自變數/預測變數/獨立變項/特徵)與連續型Y(依變數/反應變數)之間關係的模型，其中線性(Linear) 指的是利用X之間的線性組合建構模型，簡單來說是想要找到一條最好的直線描述X與Y之間的關係。線性迴歸雖然相對簡單，但卻是許多方法的發展基礎，後面許多較複雜方法可以發現是線性迴歸模型的延伸或拓展。

"迴歸"這個名詞最一開始是由英國的遺傳學與優生學家Francis Galton所提出，或許是受到表哥達爾文的影響，Galton也熱衷於遺傳與演化的學問研究，他當時在1886年討論身高遺傳性的論文中首度發展了迴歸的統計方法。他發現：「非常高的父母所生的小孩通常會比父母矮，而非常矮的父母所生的小孩通常會比父母高。」他將這個現象稱為「向平均值迴歸(regression toward the mean)」，使得後世的人就將這個方法稱為迴歸。現今的線性迴歸也是針對資料的平均值行為做的預測模型，這幾天的內容會先從簡單線性迴歸(simple linear regression)講起，再延伸到參數的估計方法與正規化(regularization)。

以下是幾個我們想利用線性迴歸模型尋找答案的問題：

• 資料Y與X之間是否存在線性關係
• 若Y與X存在關係，這個關係有多強
• 預測出的Y準確度有多高

簡單線性迴歸(Simple Linear Regression)

簡單線性迴歸模型是指只利用一個解釋變數X預測反應變數Y的線性迴歸模型，其中Y為連續型的變數，X可以是連續或類別的變數，而模型中Y沒有辦法以X解釋的部分就會落在誤差項(error term)，以下是模型架構：

• 資料：(, ), (, ), ..., (, )

• 模型： , where ,

• 參數：(截距), (斜率) ,

• 模型假設：

  1. 解釋變數X與反應變數Y之間的關係為直線的(linear)
  2. 樣本之間互相獨立(independent)
  3. Y在X的任一個數值下都服從常態分佈，且變異數為一個常數

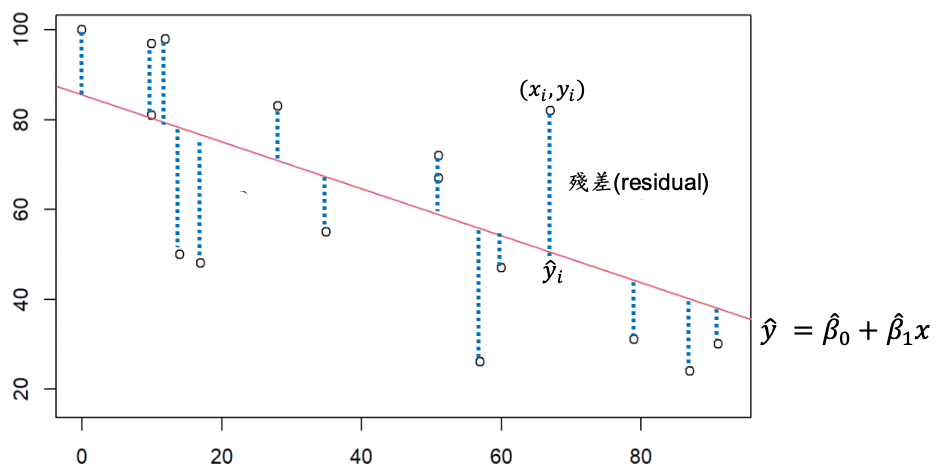
• 示意圖：
  白點為我們收集到的資料()，參數上方有hat的符號表示為估計值，有了上述模型下的三數估計值就可以畫出一條直線，其中紅色直線是以簡單線性迴歸模型找出最能夠描述資料的直線。藍色虛線為殘差(residual)，是模型估計值與資料的差距，殘差也可以想成誤差的估計值。殘差在迴歸模型中可以用來估計參數，也可以利用殘差分析(residual analysis)檢查上述幾項模型假設。
  

簡單線性迴歸參數估計：

在上述的模型架構下我們最感興趣的參數為迴歸係數與 ，而線性迴歸模型的核心概念是要找到一條最適合的直線，因此在估計模型參數時最常利用到的方法為最小平方估計法(Least Square Estimation, LSE)，使每個資料點與直線的垂直距離平方和最小，換句話說就是使殘差的平方和(Residual Sum of Squares, RSS)最小。

• 殘差(residual)：
• 殘差平方和(RSS)：

接著以微積分的技巧針對上述RSS式子求解可以得到參數的估計解：

其他常見的方法還有最大概似估計法(Maximum Likelihood Estimation, MLE)以及梯度下降法(Gradient Descent)。最大概似估計法是利用模型中對於殘差項的分佈假設進行求解的方法，在殘差項被我們假設為常態分佈時，所得到的結果會與最小平方法一致。梯度下降法是一種利用迭代求解的方法，在機器學習中常常會定義Lost function以梯度下降法的迭代來"訓練"出最適合的模型參數，在線性迴歸模型中也可以利用這樣的概念求解參數，其中的殘差平方和就可以當成Lost function接著利用梯度下降法找出參數。最小平方法或最大概似估計法可能沒有辦法在每種模型甚至高維度時，找到參數的解析解(closed-form)，因此梯度下降法在某些情境下是更受歡迎的方法。

小結

線性迴歸模型是監督式學習的迴歸中，是最常見也最為被廣泛使用的方法，而今天介紹的簡單線性迴歸模型是建立一個解釋變數X如何影響反應變數Y的模型，也就是藉由這個模型了解當X變化時，Y會隨著X如何變化。接下來幾天的內容將會讓大家了解更多線性迴歸模型的運作機制與議題。