前言

支持向量機(Support Vector Machine, SVM)，是Vladimir Vapnik在 1960 年代首次開發的一類統計模型。在近幾年，該模型已大大發展成為最靈活和最有效的機器學習工具之一。屬於一種監督式學習的方法，可用於處理分類以及迴歸的問題，但目前大多的討論在於分類的問題。

假設在兩類的分類問題中，在直覺上最直接的想法應該可以利用一條直線或平面將兩類資料分開，但這種方式僅限於資料可以完美被分開的情況。若資料沒辦法利用一條直線或平面來分開，則SVM透過非線性的函數轉換就將資料投射到更高維度的空間，找到能使資料分開的線性最佳的分離平面(linear optimal separating hyperplane)。

超平面(hyperplane)

在p維度的空間中，hyperplane就是p-1維度的平面子空間。例如在二維空間中的hyperplane為一條直線、三維空間的hyperplane為一個平面(2維子空間)。在高中數學也有談論到空間中的平面問題，一個平面就是所有維度的線性組合，例如：，法向量(normal vector)為(a, b, c)。因此在p維空間的hyperplane為，法向量，滿足此數學式子表示資料點在這個平面上，而大於0或小於0表示在平面的兩側，因此利用這個數學上的特性就能以資料代入式子為正或負來進行分類。

例如下圖定義藍色資料點的標籤；紫色為 ，假設可以使資料完美分隔為兩類的separating hyperplane為。為上方藍色資料點，為下方紫色資料點，因此separating hyperplane特性是。另外，數值的大小也可以得知該資料點距離平面的距離，也就是說數值與0越接近表示資料點離平面越近。

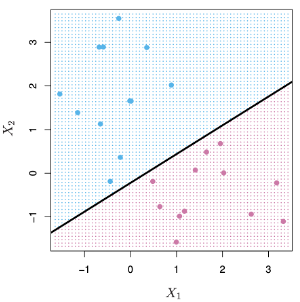
事實上若要將上圖這種兩類資料完美的分離有無限多條線可以符合這樣的條件，因此接下來的問題是：這些直線哪一條是最好的，這個問題等同於在問：哪一條直線可以在測試資料集有最小的分類錯誤率。例如下圖中三條直線都可以將藍色與紅色的資料點分開，但是否有一條直線表現的表另外兩條還好？如果一條線距離任何一類的資料點太近，那麼那條直線將對一個或多個點的微小變化更敏感。例如紅線靠近紅色資料點，藍線接近藍色資料點，如果紅點稍微改變位置，它可能會落在紅線的另一側。同樣地，如果藍點的位置稍有變化，它可能會被錯誤分類。藍線和紅線都對觀測值的微小變化更敏感。然而，黑線距離兩類資料距離都比較遠，對於資料變化不會太敏感，在測試集資料可能會優於藍線與紅線。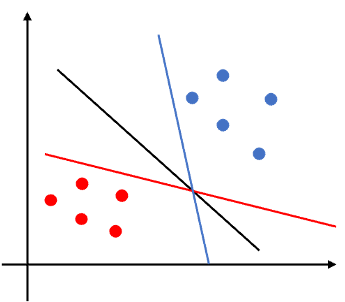

Optimal Separating Hyperplane

Optimal separating hyperplane或稱為最大邊距分類器(Maximal Margin Classifier)，就是為了處理上述有無限多條直線或平面可以將資料分離的問題，找出最適合的直線或平面，例如上圖的黑線距離是可以將兩類資料分開且距離最遠的直線。其中Margin指的是資料到平面的垂直距離。因此最好的separating hyperplane是：資料中每個資料點到這個平面的距離要大於等於M，且能符合這個條件最大的M就是最好的separating hyperplane。例如下圖的黑線就是能符合這些條件的optimal separating hyperplane。

在黑色虛線(邊界)上的三個資料點與最好的分離平面等距，到平面距離為M，稱為支持向量(support vector)，因為他們是在p維空間中的向量點，且支持了optimal separating hyperplane，也就說只要這些支持向量稍微移動，這個最好的平面也將會移動。可以發現，optimal separating hyperplane直接由這些支持向量所決定，不取決於其他觀測資料點。Optimal separating hyperplane僅直接取決於資料的一小部分這個特性，是這幾天討論支持向量分類器(Support Vector Classifier)和支持向量機(Support Vector Machine)時，利用到的一個重要屬性。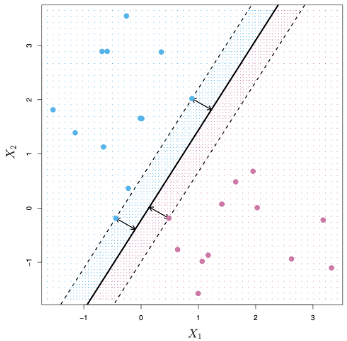

• 數學定義(可利用Lagrange Function求解)：
  

小結

如果存在separating hyperplane，最大邊距分類器的方法是一種非常直覺的分類分法。 然而，在許多情況下可能不存在separating hyperplane，因此不存在最大邊距分類器。也就是資料沒辦法使用一個線性的直線或平面來分類。在這種情況下，上述的最佳化問題沒有M>0的解。然而，明天的內容將會提到支持向量分類器(Support Vector Classifier)與支持向量機(Support Vector Machine)，可以擴展separating hyperplane的概念，使用所謂的soft margin找到一個幾乎可以將所有資料分類完善的超平面。最大邊距分類器對沒辦法完全分離的資料情況的推廣稱為支持向量分類器。

參考資料與圖片來源：
An Introduction to Statistical Learning